APR/AER/EAR

Interest rates are usually quoted as an annual rate, referred to as the nominal rate, but interest could be paid over any period, e.g. daily, monthly, quarterly or half yearly, rather than at the end of the year.
Having the interest paid at different intervals will impact the future value.
To calculate the impact of different payment intervals we need to find the EAR/APR/AER using the following formula.
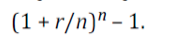
An Example:
A sum of £15,000 is invested for 5 years at a bi-annual rate of 4%. Calculate the APR and the value that will be accumulated after 5 years.
-First we need to calculate the APR, for this we need the interest rate (4%) and time period (2 as twice yearly). We can then place these figures into the APR formula. This gives us a figure of 0.0404 or 4.04%.
-Now that we are aware of the APR we can use this to calculate the future value with the additional information of present value (15,000) and time period (5 as accumulated for 5 years).
-To do so we then place these figures into the compound interest formula which gives us an accumulated value after 5 years is £18,284.92 at an APR of 4.04%.
Questions - Use Your Note Taker To Jot Down Ideas / Calculations
- A sum of £10,000 is invested for 4 years at a bi-annual rate of 3%. Calculate the APR and the value
that will be accumulated after 4 years.
a) £10,450.34
b) £12,457.84
c) £11,263.83
d) £11,679.54
C)
First the APR needs to be calculated. For this we need the interest rate 0.04 and the time period 2
(twice yearly).
(1 + 0.03/2) ^ 2 – 1
These figures put into the APR formula gives us a figure of 0.0302 or 3.02%.
Next this APR figure needs to be used in the compound interest formula to calculate the future
value.
FV = £10,000 (1 + 0.0302) ^ 4
This gives us a future value of £11,263.83
2. A sum of £15,000 is invested for 3 years at a quarterly rate of 6%. Calculate the APR and the value
that will be accumulated after 3 years.
a) £17,936.12
b) £16,435.34
c) £17,864.32
d) £18,687.54
A)
First the APR needs to be calculated. For this we need the interest rate 0.06 and the time period 4
(quarterly).
(1 + 0.06/4) ^ 4 – 1
These figures put into the APR formula gives us a figure of 0.0614 or 6.14%.
Next this APR figure needs to be used in the compound interest formula to calculate the future
value.
FV = £15,000 (1 + 0.0614) ^ 3
This gives us a future value of £17,936.12
- Further Study Text: Pages 158 - 160